SICP Goodness - What is Meant by Data? (II)
Just a little bit of lambda calculus

Do you think Computer Science equals building websites and mobile apps?
Are you feeling that you are doing repetitive and not so intelligent work?
Are you feeling a bit sick about reading manuals and copy-pasting code and keep poking around until it works all day long?
Do you want to understand the soul of Computer Science?
If yes, read SICP!!!
This is the second part of a two part series, you can find the first part here.
The main topic of this post is Church Encoding.
Boolean
How to build Boolean value true and false using only functions?
Let’s take a look at the general idea of a boolean.
if bool ? first : second
So here we see that the practical meaning of a boolean is to make choices. The program does not care whether something is really true or not, it only need to use it to make choices.
The above example code says that if bool is TRUE, it returns first, else returns second. This sounds very familiar, yes, they are K and KI. So actually we already have boolean functions.
(define T K)
(define F KI)Not
The Not function takes T returns F and vice versa.
;; NOT := λp. p F T
(define (NOT p) ((p F) T))Just try the NOT function, it actually works.
There is another way to think about NOT. T is a function that returns the first argument, and F is function that returns the second argument. Imagine after applying NOT to them, T will return the second argument and F will return the first argument. So NOT changes the behavior of T and F, as if the order of the arguments have been switched. Emmm, what function switches arguments?
C. So C is NOT.
And
;; AND := λpq. p q p
(define (AND p)
(lambda (q)
((p q) p)))Try all 4 combinations and prove that this is actually AND.
Or
Similar to AND, OR is:
;; OR := λpq. p p q
(define (OR p)
(lambda (q)
((p p) q)))If we ignore the q here, then OR becomes M! Actually they behave the same way. You can try it yourself.
OK, enough logic, let’s talk about numbers.
Numbers
To define numbers as function, we need to make some slight changes. Instead of one two three, we are using once twice thrice. Because of reasons ;)
;; N1 := λfa. f a
(define N1
(lambda (f)
(lambda (a) (f a))))N1 is a function that takes f and a and calls f once on a.
And N2 can be defined similarly as:
;; N2 := λfa. f (f a)
(define N2
(lambda (f)
(lambda (a) (f (f a)))))
N2 calls f twice on a.
Let’s also define N3 here.
;; N3 := λfa. f (f (f a))
(define N3
(lambda (f)
(lambda (a) (f (f (f a))))))
I think you get the idea, our number system is defined by how many times we apply a function f to an argument a.
What is 0? It is calling f on a zero times.
;; N0 := λfa.a
(define N0
(lambda (f)
(lambda (a) a)))Wait, N0 looks familiar, it is KI or F.
Also look back at N1 := λfa. f a, if we see f a as together, then N1 is I.
So 0 is false and 1 is identity, this should’ve put a smile on your face.
SUCC
A SUCC function will add 1 to a given number.
SUCC N1 = N2
SUCC N2 = N3
SUCC (SUCC N1) = N3
...It is not very straightforward to implement SUCC, so let’s take it slowly.
First, SUCC should take a church number n and returns a new church number.
SUCC := λnfa.??
The new church number is simply calling f once more. So we can just call f n times on a first, and then call f on the result.
SUCC := λnfa.f(nfa)
(define SUCC
(lambda (n)
(lambda (f)
(lambda (a)
(f((n f) a))))))Now to verify all these, let’s translate the church numbers into real numbers.
The function to_real_numbers takes a church number n andf calls it with plus one funcation as f and 0 as a. For example, N2 now means increase 1 twice on 0.
(define to_real_number
(lambda (n)
((n (lambda (x) (+ x 1))) 0)))Blue Bird
Next, let’s introduce another bird: Blue Bird.
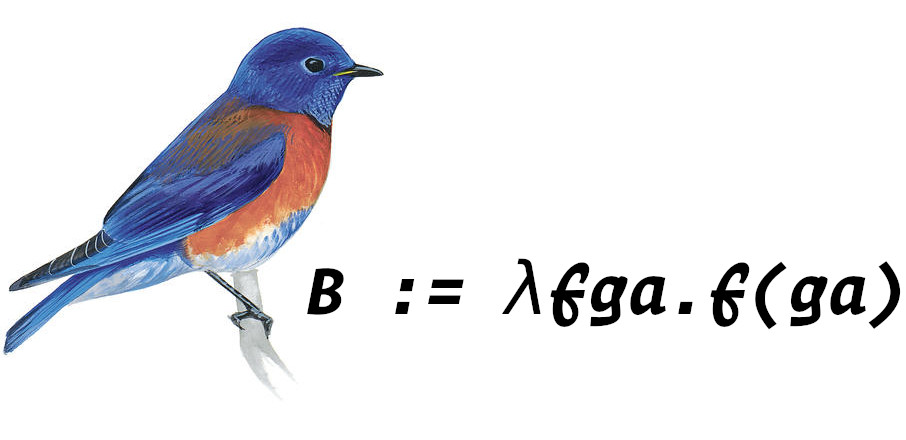
B acts like a function pipeline, or function composition.
Apply the outer most function with a, take the result and pass it as a parameter for inner function, and keep doing this until there is no inner function anymore.
(define B
(lambda (f)
(lambda (g)
(lambda (a)
(f (g a))))))For example
;; the pipeline is N1 -> N2 -> 2
(((B to_real_number) SUCC) N1)ADD
How to implement ADD?
(ADD N0 N3) = N3
(ADD N1 N3) = (SUCC N3)
(ADD N2 N3) = (SUCC (SUCC N3))We can see add n to a can be seen as apply n times SUCC on a.
;; ADD := λnk.n SUCC k
(define ADD
(lambda (n)
(lambda (k)
((n SUCC) K))))MULT
Again let’s use the example of (MULT N2 N3).
We know the result should be N6, which means apply some f 6 times on some a.
But we can also say that it applies f 3 times twice.
;; MULT := λnkf.n(kf)
(define MULT
(lambda (n)
(lambda (k)
(lambda (f)
(n (k f))))))Wait a moment, look at the definition above, it is identical to B. So MULT is actually B!
I think we have come quite far. If you now look back at the Ex.2.6 mentioned in Part I, we not only can answer how to implement ADD, we know how to implement MULT too!

Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Email