SICP Goodness - What is Meant by Data? (I)
Just a little bit of lambda calculus

Do you think Computer Science equals building websites and mobile apps?
Are you feeling that you are doing repetitive and not so intelligent work?
Are you feeling a bit sick about reading manuals and copy-pasting code and keep poking around until it works all day long?
Do you want to understand the soul of Computer Science?
If yes, read SICP!!!
Let’s begin by asking the question: What is data? You may say that data is numbers, characters, strings, pairs, lists, maps, sets and so on. Then, what is procedure?. Well a procedure is a function that can be called with(out) parameters.
What if I tell you that data can be procedures?
For me, the first really mind boggling example in the book is this:
(define (pair x y)
(define (dispatch m)
(cond ((= m 0) x)
((= m 1) y)
(else (error "Argument not 0 or 1"))))
dispatch)
(define (frst p) (p 0))
(define (snd p) (p 1))This is a working pair data structure that is implemented only using functions. Function pair is used to make a pair, and frst selects its first item, and snd selects its second item.
;; 1
(fsrt (pair 1 2))
;; 3
(snd (pair 2 3))In exercise 2.4, an alternative way of implementing pair is given as follows.
(define (pair x y)
(lambda (m) (m x y)))
(define (frst p)
(p (lambda (a b) a)))
(define (snd p)
(p (lambda (a b) b)))If you have no problem understand these, then take a look at exercise 2.6:
In case representing pairs as procedures wasn’t mind-boggling enough, consider that, in a language that can manipulate procedures, we can get by without numbers (at least insofar as nonnegative integers are concerned) by implementing 0 and the operation of adding 1 as
(define zero (lambda (f) (lambda (x) x)))
(define (add-1 n)
(lambda (f) (lambda (x) (f ((n f) x)))))This representation is known as “Church numerals”, after its inventor, Alonzo Church, the logician who invented the [lambda] calculus.
Define
oneandtwodirectly (not in terms ofzeroandadd-1). (Hint: Use substitution to evaluate(add-1 zero)). Give a direct definition of the addition procedure+(not in terms of repeated application ofadd-1).
To be honest, this really made me want to vomit. But hold it back, maybe we can learn a bit of this so called lambda calculus first, and then revisit this problem.
I found a great talk about this topic, and I highly recommend you watch the video several times until you understand most of the things in the talk, and remember to have pen and paper at hand when you do so.
PART I
PART II
If you understand this talk, exercise 2.6 will become trivial and obvious to you.
I now will summarize the talk here.
Lambda calculus syntax
First let’s take a look at the syntax of lambda calculus. I think it’s easier to explain by examples.
;; a function that takes a and returns a
λa.a
;; equivalent form in scheme
(lambda (a) a)λa.bx
;; equivalent form in scheme
(lambda (a) (b x))(λa.b)x
;; equivalent form in scheme
((lambda (a) b) x)λa.λb.x
;; equivalent form in scheme
(lambda (a) (lambda (b) x))
;; This can also be shortened to
λab.xλa.bcx
;; equivalent form in scheme
(lambda (a) ((b c) x))Birds
Let’s now take a look at some important functions. They are all named after birds.
Idiot Bird
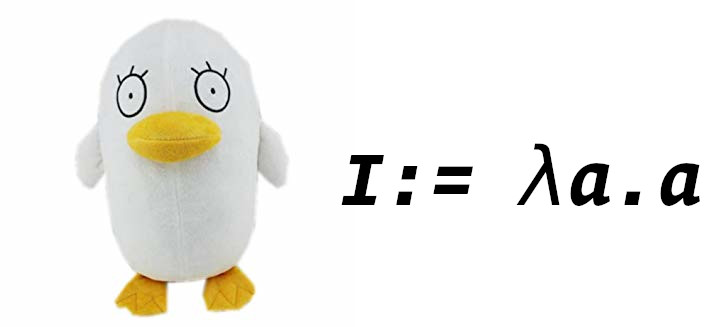
The first one is idiot bird or I for short. As its name says, it is not that smart. So it just returns what it takes. Pretty straightforward.
Let’s implement it in Scheme.
(define I
(lambda (a) a))Mocking Bird
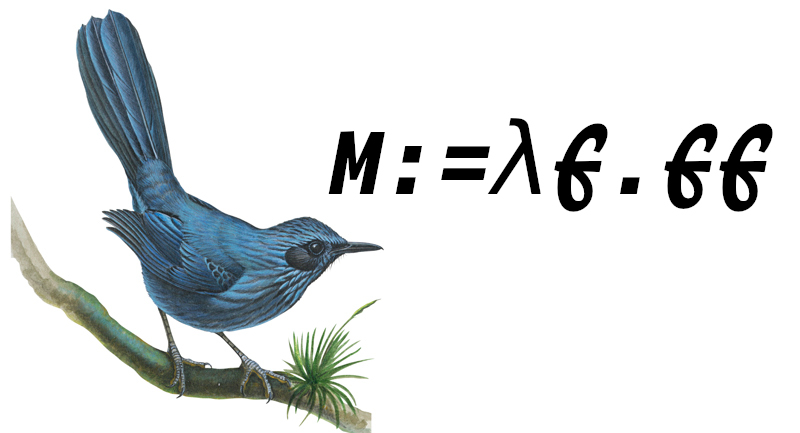
This one is pretty interesting. It takes a function, and calls it on itself.
(define M
(lambda (f) (f f)))What is M(I)?
It’s (I I) which is just I.
And what is (M M)?
Uh-oh, it is (M M) which is (M M) which is (M M) … so it never ends.
Kestrel
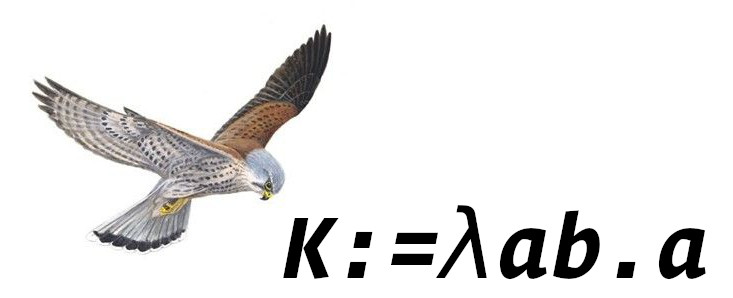
The kestrel takes a and b then returns a.
(define K
(lambda (a) (lambda (b) a)))This is the built-in function in Haskel, called const. Why const? Let’s say if we call K with 5. This will return a new function, that no matter what you call it with, it will always return 5. Hence the name const.
Now the fun part.
K I x = I
Each side of the equation is a function, so we can do the following:
K I x y = I y
We add y to both sides. Since I y always returns y, we will then get
K I x y = y.
If we see K I as one function, then what K I does is that it takes x and y then returns y.
So K I is opposite to K.
This is actually not hard to understand.
As we already know, if you call K with only one parameter x, it returns a constant x function. So K I will return a function that will always return I. So K I a = I, then call it with b will get K I a b = I b = b.
So we just derived Kite.
Kite

(define KI
(lambda (a) (lambda (b) b)))This is the opposite of Kestrel.
Now let’s look at a new bird: Cardinal.
Cardinal
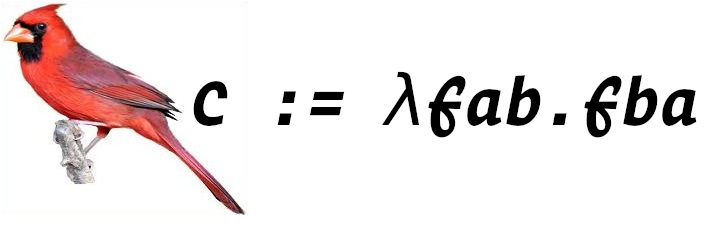
Cardinal takes a function and two parameters, but calling them in different order.
(define C
(lambda (f)
(lambda (a)
(lambda (b) ((f b) a)))))Let’s see an example. What is C K I M?
C takes in a function K and two parameters I and M and calles them in different order which is K M I = M.
Emm, so C K I M = M, if we see C K as a new function. Then C K is KI! You can type in the scheme code and prove this yourself.
OK, I think we have introduced enough birds, and this post is getting too long so I will stop here. In part II, we will continue and talk about what is Church Encoding. And then get back to our SICP exercise.
Stay tuned!

Share this post
Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Email