Tree Vs Iterative Fibbonacci Numbers

Two types of recursion

2 minute read

Being a programmer, you should be very familiar with Fibbonacci numbers. It is often being introduced when teaching recursion.

Tree Recursion

Most likely the implementation of a function that calculate fib number is as follows:

(defn fib-tree [n]
  (cond (= n 0) 0
        (= n 1) 1
        :else (+ (fib-tree (- n 1)) (fib-tree (- n 2)))))

This is just a direct translation from the Fibonacci number definition. Since it is straightforward and easy to understand, most textbooks use it as an typical example for illustrating recursive function. But, very few provide deeper discussions about it.

Yes, this is a recursive implementation, but it is a so called Tree Recursion. What does it mean? Let’s take a closer look together and go through the execution path.

Let’s first take the simplest case, (fib-tree 0) and (fib-tree 1), the function directly returns 0 and 1 separately.

What about (fib-tree 2), so in order to get (fib-tree 2) we need to first get (fib-tree 1) and (fib-tree 0), which we already know from above. So, fair enough.

Now let’s try (fib-tree 3). We now need (fib-tree 2) and (fib-tree 1). And in order to get (fib-tree 2), we need (fib-tree 1) and (fib-tree 0). Now pay attention here, we calculate (fib-tree 1) twice.

As a matter of fact, the bigger the n is, the more duplicate calculations there will be. And it looks like a tree as follows.

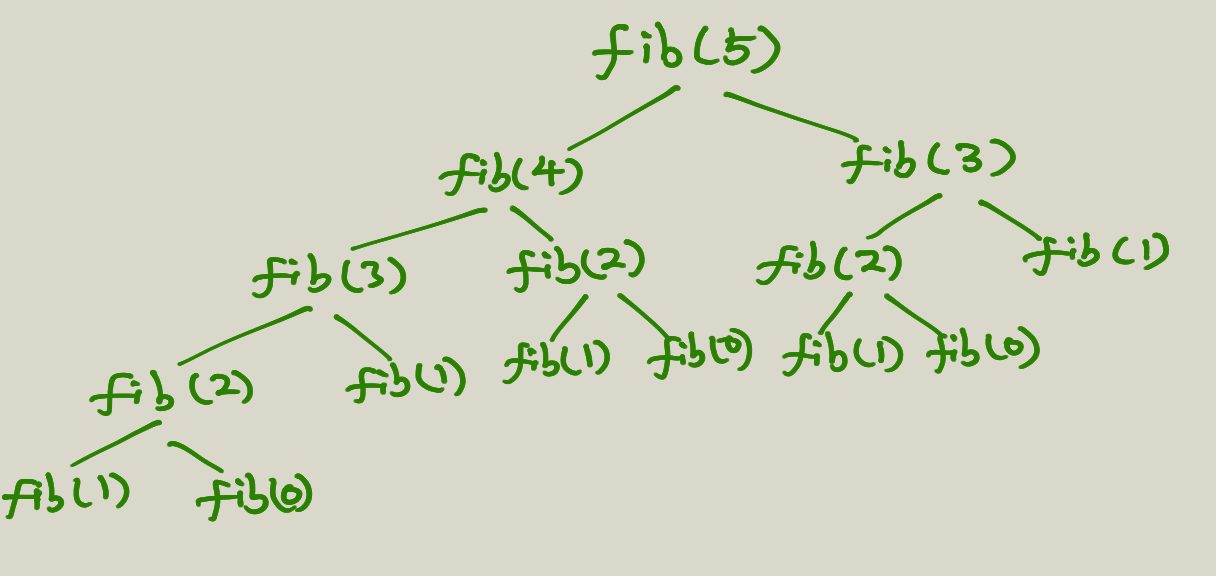
Fib Tree

Not only there are a lot of duplicate calculations, but also each level of the tree means a call stack in memory. So this implementation is actually really bad, cause it uses a lot memory and wastes a lot of calculations. Is there a better way?

Iterative Recursion

The answer is yes. Turns out we only need 2 variables for calculating Fib number. One for the current fib number, one for storing the previous fib number in order to calculate the next one. The code looks like:

(defn fib [n]
  (loop [a 0
         b 1
         count n]
    (if (<= count 0)
      a
      (recur (+' a b) a (dec count)))))

If you are still confused like I was the first time, here is a illustration.

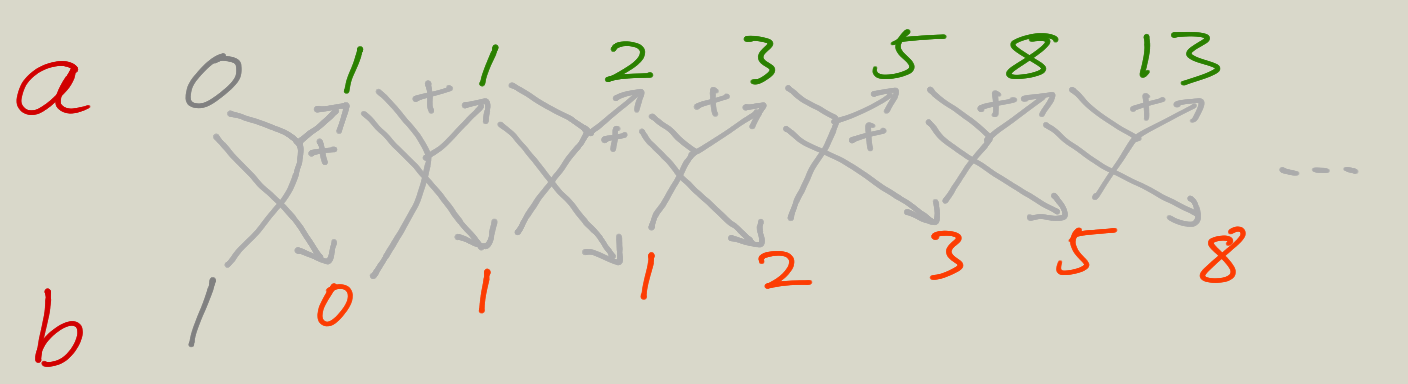
Fib Tree

Here we have only two variables in memory and no wasted calculations.

Conclusion

The performance of these two implementations is very big. I timed on (fib 40) on both implementations, here are the result:

For tree version: “Elapsed time: 23647.536245 msecs”

For iterative version: “Elapsed time: 0.099965 msecs”

So the verdict is, try to come up with a iterative version of recursion as much as possible.

comments powered by Disqus