SICP Goodness - Stream(11)

Solving differential equations

Guowei Lv

3 minute read

Do you think Computer Science equals building websites and mobile apps?

Are you feeling that you are doing repetitive and not so intelligent work?

Are you feeling a bit sick about reading manuals and copy-pasting code and keep poking around until it works all day long?

Do you want to understand the soul of Computer Science?

If yes, read SICP!!!

In last article we talked about the integral procedure. In this article, we talk about how to use it to solve differential equations.

First let’s make sure we understand the math. Actually we do not need to open your 1000 page calculus textbook and start reading from page 1. To understand the example in the book we simply need to know how to solve that one differential equations:

y' = y

Let me put this in English: we are trying to find a function y, which the derivative of y is equal to y itself.

We do not even need to know how to solve this ourselves, there are many online tools to help us. So the result of this is

y = e^(x + C)

This is all the math we need to know to continue.

Next we will explain how to solve y' = y using the integral procedure.

There is a Henderson Figure given in the book:

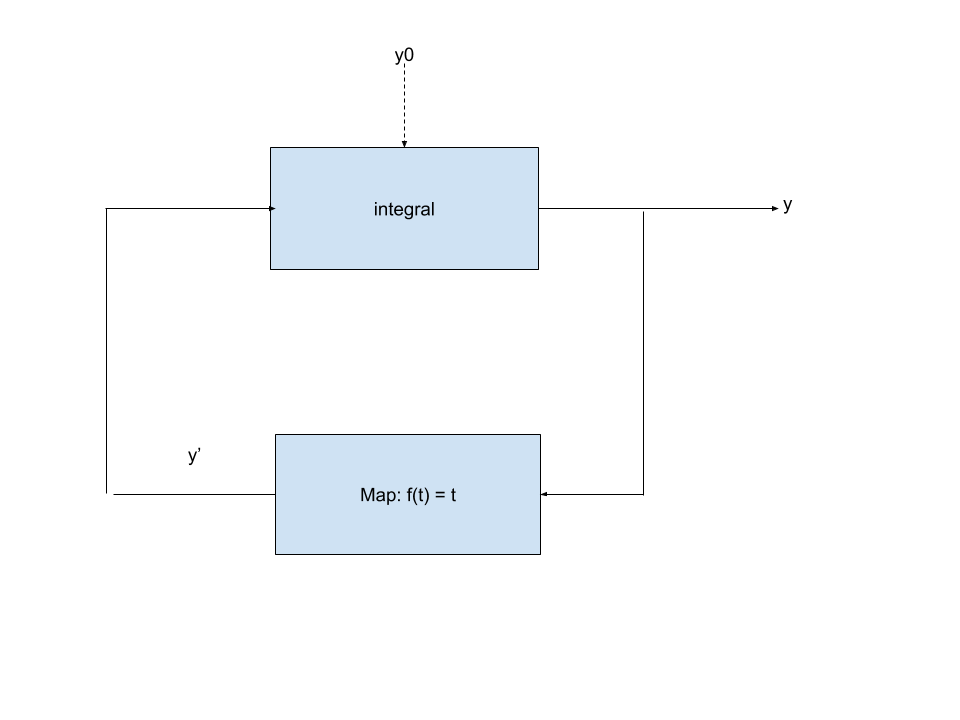
To understand this figure, we can divide it into the upper part and the lower part.

The upper part says is just the integral procedure. It takes in the stream of derivative of y and output the stream of y itself.

The lower part describes the equation y = y' by using the stream map function f(t) = t.

Now let’s try out the solve procedure from the book. y0 = 1, dt = 0.001.

(define (integral delayed-integrand initial-value dt)
  (define int
    (cons-stream initial-value
                 (let ((integrand (force delayed-integrand)))
                   (add-stream (scale-stream integrand dt)
                               int))))
  int)

(define (solve f y0 dt)
  (define y (integral (delay dy) y0 dt))
  (define dy (stream-map f y))
  y)


(stream-ref (solve (lambda (y) y) 1 0.001) 1000)

;Value: 2.716923932235896

Acually, by following the Henderson figure, we can figure out what the y stream looks like by hand.

1

1 + dt

1 + dt + (1 + dt)dt

1 + dt + (1 + dt)dt + (1 + dt + (1 + dt)dt)dt

... ...

So we can simply write solve in the following form:

(define (solve f y0 dt n)
  (define (s f y0 dt n r)
    (if (= n 0)
        r
        (s f y0 dt (- n 1) (+ r (* (f r) dt)))))
  (s f y0 dt n y0))
  
(solve (lambda (x) x) 1 0.001 1000)
;Value: 2.716923932235896

We can see that the result is the same.

comments powered by Disqus