SICP Goodness - Stream (10)
integral using stream

Do you think Computer Science equals building websites and mobile apps?
Are you feeling that you are doing repetitive and not so intelligent work?
Are you feeling a bit sick about reading manuals and copy-pasting code and keep poking around until it works all day long?
Do you want to understand the soul of Computer Science?
If yes, read SICP!!!
Let’s talk about the integral example in the book.
This has always been a problem for me, whenever I get here, I either give up or pretend that I get it and move on. Not this time!
Let’s put the example here first for your reference.
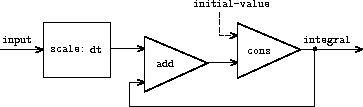
And this is the mathematical formula:
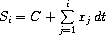
And the code:
(define (integral integrand initial-value dt)
(define int
(cons-stream initial-value
(add-stream (scale-stream integrand dt)
int)))
int)In order to fully grasp this, we need to refresh on what is integral.
In my own words, it basically represents the area between the function and x-axis. For example, the following picture shows the integral of a certain function f(x) between a and b.
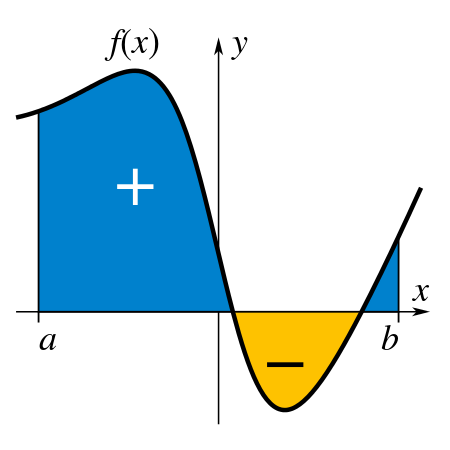
But computational wise, how to we calculate this?
One simple way is to model this function into many many thin rectangles. Then, the sum of the area of these rectangles can be used as an approx. of the area of the function.
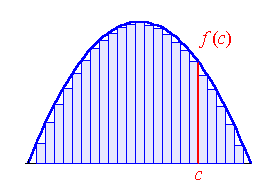
If you have difficulty understanding this, please watch this excellent video:
Example 1
Let’s now play with the integral procedure a little bit and see if we can actually use it to do something.
The simplest function that we can test is the function f(t) = 1.
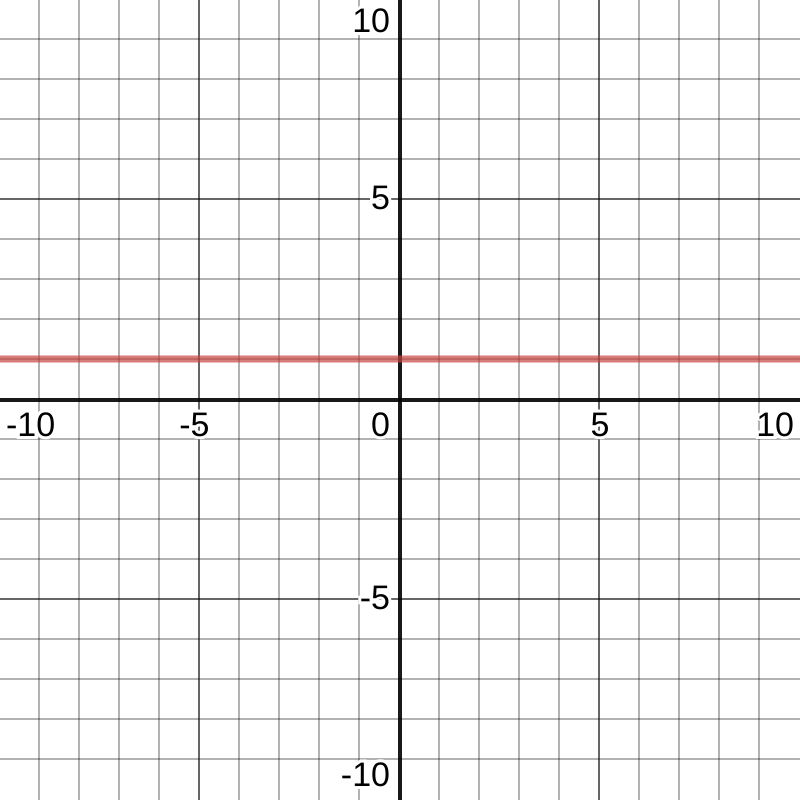
We already know its integral is function f(t) = t.
Now let’s verify this using the integral procedure.
We need to figure out what are the arguments integrand, initial-value and dt.
integrand is simple, it is just the stream ones we have define previously.
initial-value should be 0.
dt let’s set it to 0.001.
Let’s say we want to calculate the integral of the function between 0 and 1. Since dt is 0.001, that means we need 1000 values to reach t = 1.
(stream-ref (integral ones 0 0.001) 1000)
;Value: 1.0000000000000007To calculate the integral of the function between 0 and 2. We need 2000 items from the input stream.
(stream-ref (integral ones 0 0.001) 2000)
;Value: 1.9999999999998905Let’s try more,
(stream-ref (integral ones 0 0.001) 3000)
;Value: 2.9999999999997806
(stream-ref (integral ones 0 0.001) 4000)
;Value: 3.9999999999996705These values do fit the function f(t) = t nicely.
Example 2
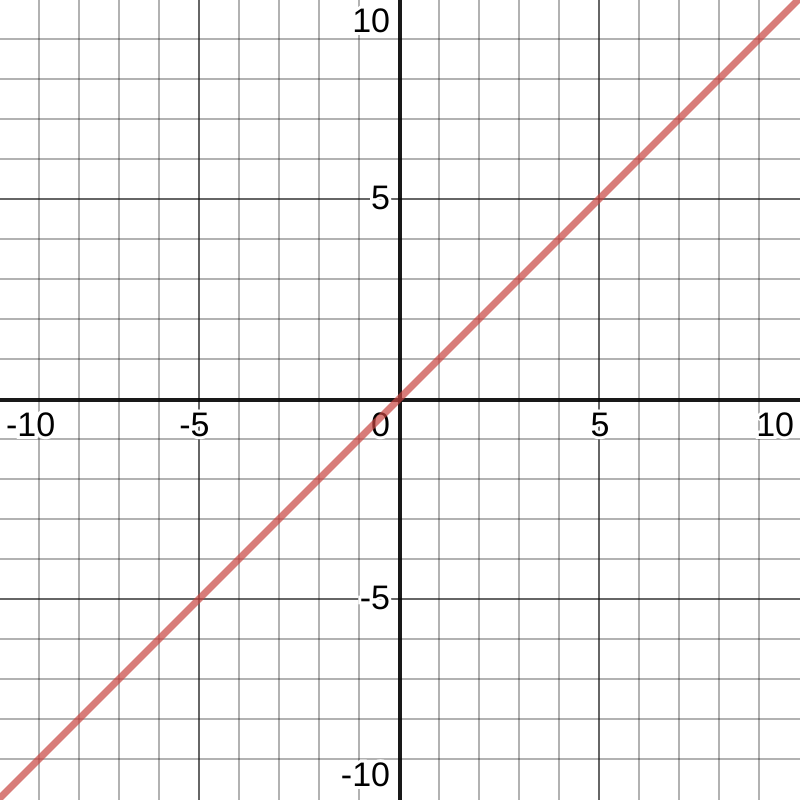
Now let’s try to integral the function f(t) = t.

We know that the integral is f(t) = 0.5t^2.
Let’s try the integral procedure.
Most important thing is to figure out what is the integrand.
The integrand is a stream of values f(t), where t is a stream of values that determined by dt.
Say if we use dt = 0.001, then t will be a stream of values of 0, 0.001, 0.002, 0.003 ... and f(t) will be a stream of values of 0, 0.001, 0.002, 0.003 ....
Now we know that the input stream will be the integers stream scaled by 0.001.
Let’s now see if the integrals are like the function f(t) = 0.5t^2.
(stream-ref (integral (scale-stream integers 0.001) 0 0.001) 1000)
;Value: .5005000000000002
(stream-ref (integral (scale-stream integers 0.001) 0 0.001) 2000)
;Value: 2.001
(stream-ref (integral (scale-stream integers 0.001) 0 0.001) 3000)
;Value: 4.5015And indeed they are.
I hope now you have a better understanding of the integral procedure.

Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Email