SICP Goodness - Mutable Data (I)
Modeling with mutable data

Do you think Computer Science equals building websites and mobile apps?
Are you feeling that you are doing repetitive and not so intelligent work?
Are you feeling a bit sick about reading manuals and copy-pasting code and keep poking around until it works all day long?
Do you want to understand the soul of Computer Science?
If yes, read SICP!!!
Mutable List Structure
We introduce 2 operations to change a list: set-car! and set-cdr!. They should be rather self-explanatory. Let’s go straight into exercises.
Exercise 3.12
The following procedure for appending lists was introduced in section 2.2.1:
(define (append x y)
(if (null? x)
y
(cons (car x) (append (cdr x) y))))Append forms a new list by successively consing the elements of x onto y. The procedure append! is similar to append, but it is a mutator rather than a constructor. It appends the lists by splicing them together, modifying the final pair of x so that its cdr is now y. (It is an error to call append! with an empty x.)
(define (append! x y)
(set-cdr! (last-pair x) y)
x)Here last-pair is a procedure that returns the last pair in its argument:
(define (last-pair x)
(if (null? (cdr x))
x
(last-pair (cdr x))))Consider the interaction
(define x (list 'a 'b))
(define y (list 'c 'd))
(define z (append x y))
z
;; (a b c d)
(cdr x)
;; <response>
(define w (append! x y))
w
;; (a b c d)
(cdr x)
;; <response>What are the missing “response"s? Draw box-and-pointer diagrams to explain your answer.
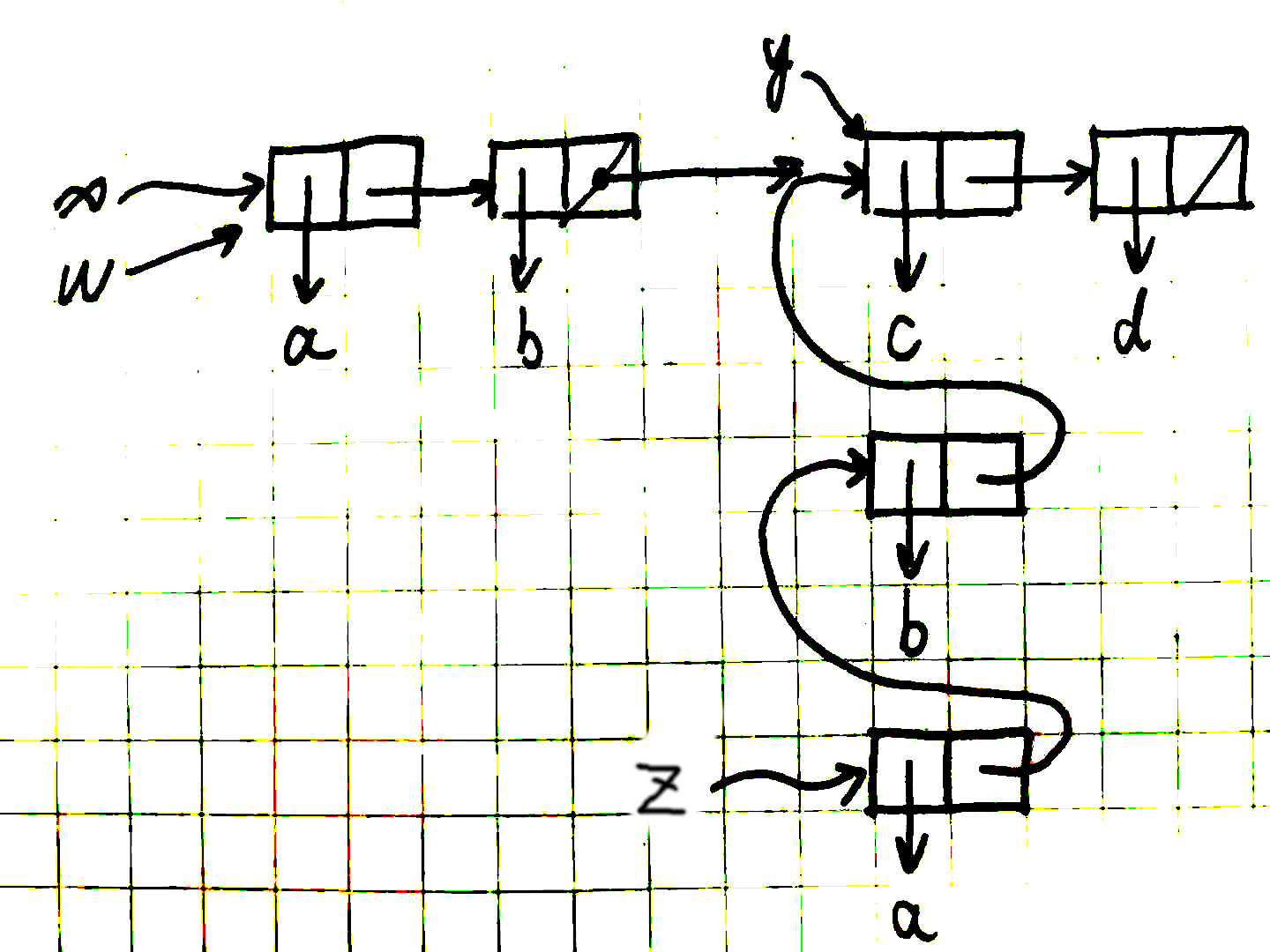
The tricky part is not in append! but in append. (append x y) is actually (cons a (cons b y)). Since cons is a constructor, it will create new box when evaluated.
Exercise 3.14
The following procedure is quite useful, although obscure:
(define (mystery x)
(define (loop x y)
(if (null? x)
y
(let ((temp (cdr x)))
(set-cdr! x y)
(loop temp x))))
(loop x '()))Loop uses the temporary variable temp to hold the old value of the cdr of x, since the set-cdr! on the next line destroys the cdr. Explain what mystery does in general. Suppose v is defined by (define v (list 'a 'b 'c 'd)). Draw the box-and-pointer diagram that represents the list to which v is bound. Suppose that we now evaluate (define w (mystery v)). Draw box-and-pointer diagrams that show the structures v and w after evaluating this expression. What would be printed as the values of v and w ?
The mystery is a in place reverse function.
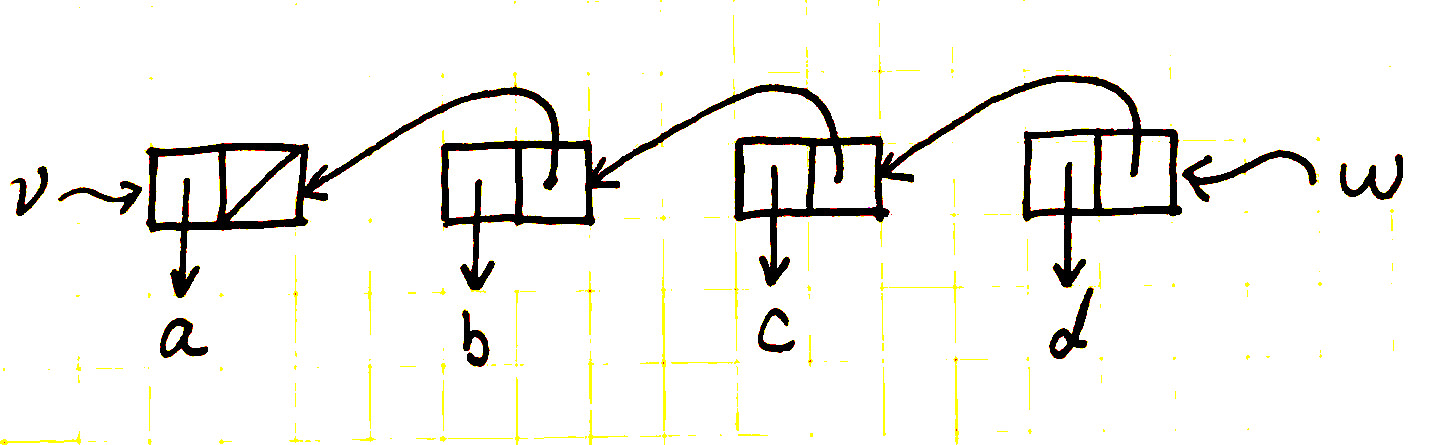
Exercise 3.16
Ben Bitdiddle decides to write a procedure to count the number of pairs in any list structure. “It’s easy,” he reasons. “The number of pairs in any structure is the number in the car plus the number in the cdr plus one more to count the curren pair.” So Ben writes the following procedure:
(define (count-pairs x)
(if (not (pair? x))
0
(+ (count-pairs (car x))
(count-pairs (cdr x))
1)))Show that this procedure is not correct. In particular, draw box-and-pointer diagrams representing list structures made up of exactly three pairs for which Ben’s procedure would return 3; return 4; return 7; never return at all.
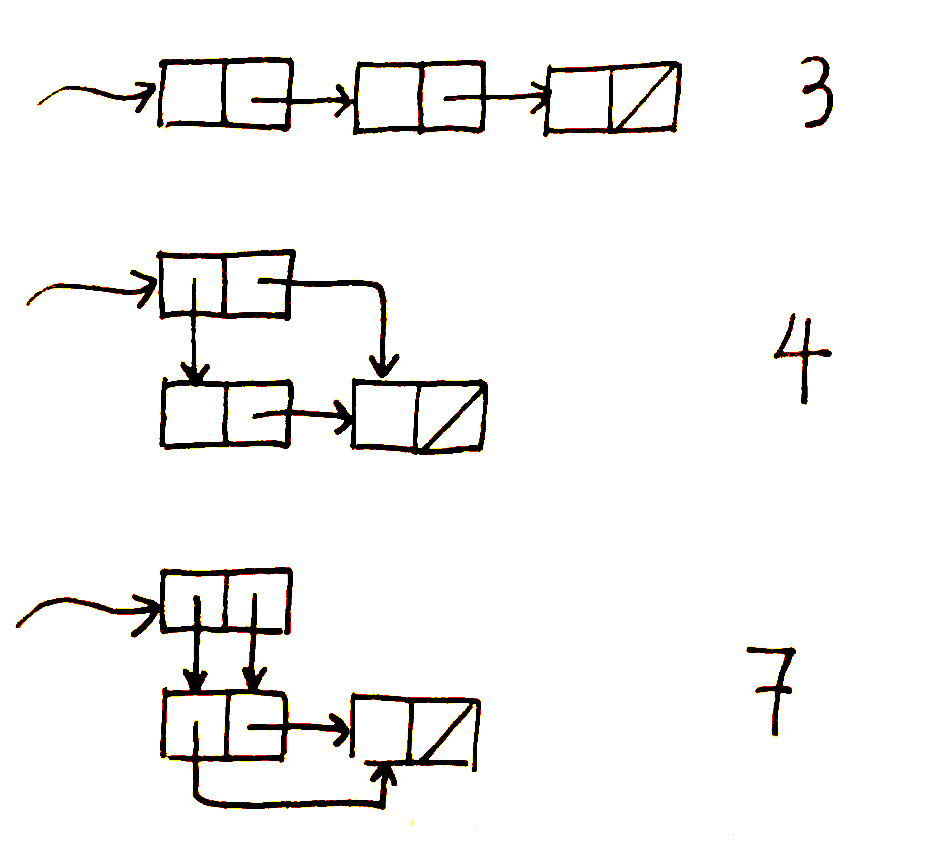
Exercise 3.17
Devise a correct version of the count-pairs procedure of exercise 3.16 that returns the number of distinct pairs in any structure. (Hint: Traverse the structure, maintaining an auxiliary data structure that is used to keep track of which pairs have already been counted.)
(define count-pairs
(let ((visited '()))
(lambda (x)
(cond ((not (pair? x)) 0)
((memq x visited) 0)
(else (set! visited (cons x visited))
(+ (count-pairs (car x))
(count-pairs (cdr x))
1))))))Notice that the let outside of the lambda, this makes the visited shared among the function recursive calls. memq will return 0 if x is not found in visited.
By doing all these exercise, we can solidify our understanding of the box-and-pointer diagrams, cause it is very base of the upcoming content.

Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Email