SICP Goodness - From Pair to Flatmap (I)

Explore the power of list

Guowei Lv

3 minute read

Do you think Computer Science equals building websites and mobile apps?

Are you feeling that you are doing repetitive and not so intelligent work?

Are you feeling a bit sick about reading manuals and copy-pasting code and keep poking around until it works all day long?

Do you want to understand the soul of Computer Science?

If yes, read SICP!!!

Sequence is an important data structure in any programming language, especially in Lisp. In this article, we will look at how it is built and what can we do with it.

Pair

Pair is a very simple data structure, it glues two objects together, and provides selectors for each of them.

In Scheme the function cons is used to create pairs. For example, (cons 1 2). This can be illustrated by using the box-and-pointer notation:

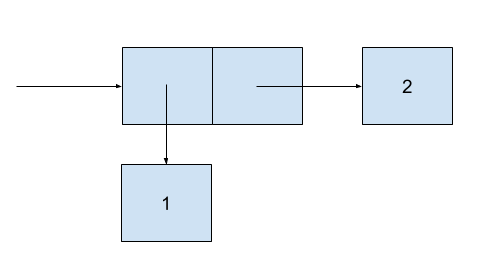
Each object is shown as a pointer to a box. The box for a primitive object contains a representation of the object. For example, the box for a number contains a number. The box for a pair is actually a double box, the left part containning the first object of the pair, and the right part containning the second one.

car is the selector for the first object and cdr is the selector for the second object.

(car (cons 1 2))

;;=> 1

(cdr (cons 1 2))

;;=> 2

Let’s say we want to combine 1, 2, 3, 4 using pairs. There are actually many ways of doing this. For example:

;; Two ways of combining 1,2,3,4 using pairs
(cons (cons 1 2) (cons 3 4))
(cons (cons 1 (cons 2 3)) 4)

They can be illustrated respectively as follows:

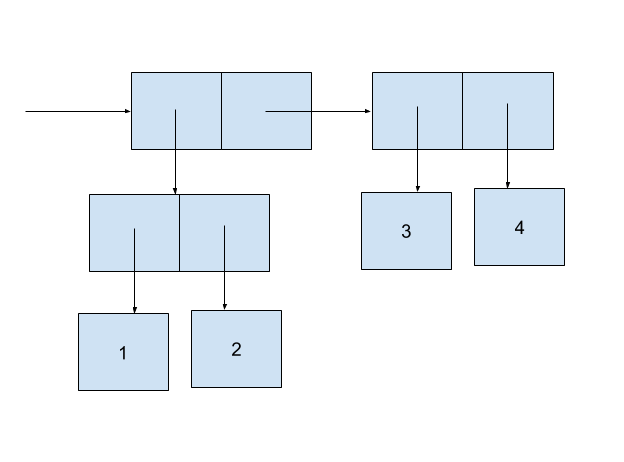
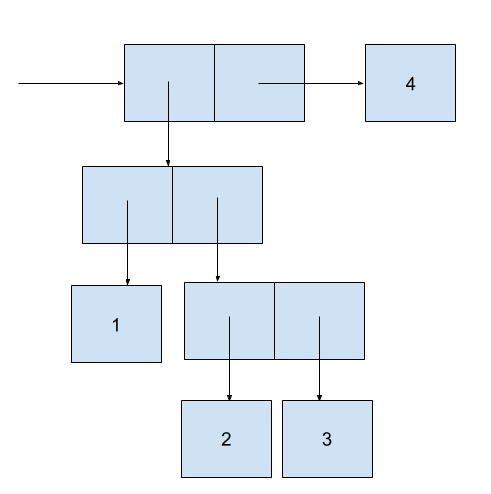
Sequence

Now we can construct sequences(an ordered collection of data objects) by chaining pairs.

For example to construct sequence of 1, 2, 3 and 4, we can do:

(cons 1 (cons 2 (cons 3 (cons 4 '()))))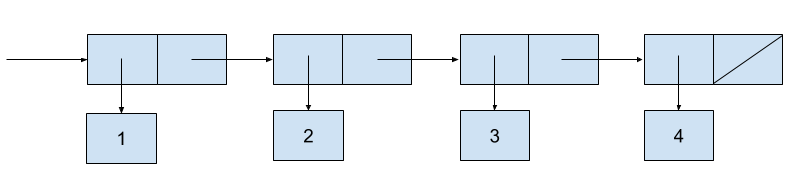

Such a sequence of pairs formed by nested cons is called a list, and Scheme provides a primitive called list to help with creating lists.

;; the followings are the same
(list 1 2 3 4)
(cons 1 (cons 2 (cons 3 (cons 4 '()))))

List Operations

car and cdr

car selects the first item in the list and cdr select the rest items (a sublist) of the list.

(car (list 1 2 3 4)) ;; 1
(cdr (list 1 2 3 4)) ;; (2 3 4)

nth element of the list

We implement this by cdring down the list and stop at the right element.

(define (list-ref items n)
  (if (= n 0)
    (car items)
    (list-ref (cdr items) (- n 1))))

The Length of the List

Sometimes we need to cdring down the whole list, so we need a way to stop. Primitive null? tells if a list if an empty list.

(null? '()) ;Value: #t
(null? (list 1 2)) ;Value #f

Now let’s implement a function to calculate the length of the list.

(define (length items)
  (if (null? items)
    0
    (+ 1 (length (cdr items)))))

We can also write a iterative version.

(define (length items)
  (define (iter items result)
    (if (null? items)
      result
      (iter (cdr items) (+ 1 result))))
  (iter items 0))

Append Two Lists

This is implemented by cons up a result list while cdring down a list.

(define (append list1 list2)
  (if (null? list1)
    list2
    (cons (car list1) (append (cdr list1) list2))))

Two exercises:

Write a function to reverse a list.

(define (reverse items)
  (if (null? items)
    '()
    (append (reverse (cdr items)) (list (car items)))))

Write a function to get the last pair in the list.

(define (last-pair items)
  (cond ((null? items) '())
        ((null? (cdr items)) items)
        (else (last-pair (cdr items)))))

Part II of this series can be found here.

comments powered by Disqus