A Little Java a Few Patterns
Java done by hardcore Lisp hackers
I got the book A Little Java, A Few Patterns not long ago and have been reading it since.
The teaching style of the book is refreshing. I do highly recommend this book if you want to learn about design patterns with a functional programming taste. Or if you simply love pizza.

The first half of the book is kind of easy for me since I already know Java and a few design patterns. But the complexity of the examples are building up quickly. There is this example of a program to evaluate expressions that I have to type the code into an IDE to understand fully, and I will put it here for later reference.
Intention
First a few words about what the program does.
The program is to evaluate expressions.
There are two types of expressions, one with numbers and one with sets. And both expressions are built using the same set of operators: plus(+), diff(-) and prod(x).
For example:
(+ 1 (- 10 (x 2 2)))is evaluated to 7.
But what about this:
(+ {5, 7} (+ (- {4} {3}) {5}))Well, we just translate each + - x to set operators union, minus and intersect.
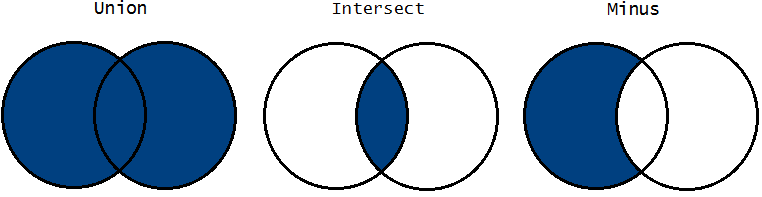
So the result of evaluating the above expression is {7, 5}.
The Program
First, we define what is an expression.
abstract class Expr {
abstract Object accept(ExprVisitor ask);
}Notice that there is no methods in this class because we are using visitor pattern here.
Now we have the base type Expr we can define different subtypes of expressions.
First of all, the most basic expression is just a constant value.
class Const extends Expr {
private Object c;
Const(Object c) {
this.c = c;
}
@Override
Object accept(ExprVisitor ask) {
return ask.forConst(c);
}
}Then, + - x are also expressions.
class Plus extends Expr {
private Expr l;
private Expr r;
Plus(Expr l, Expr r) {
this.l = l;
this.r = r;
}
@Override
Object accept(ExprVisitor ask) {
return ask.forPlus(l, r);
}
}
public class Diff extends Expr {
private Expr l;
private Expr r;
Diff(Expr l, Expr r) {
this.l = l;
this.r = r;
}
@Override
Object accept(ExprVisitor ask) {
return ask.forDiff(l, r);
}
}
class Prod extends Expr {
private Expr l;
private Expr r;
Prod(Expr l, Expr r) {
this.l = l;
this.r = r;
}
@Override
Object accept(ExprVisitor ask) {
return ask.forProd(l, r);
}
}Next, we define the interface ExprVisitor:
public interface ExprVisitor {
Object forPlus(Expr l, Expr r);
Object forDiff(Expr l, Expr r);
Object forProd(Expr l, Expr r);
Object forConst(Object c);
}This code says that any visitors used on Exprs, will have to deal with its four subtypes.
For each expression, what we want to do is to evaluate it. So let’s create a visitor Eval:
public abstract class Eval implements ExprVisitor {
abstract Object plus(Object l, Object r);
abstract Object diff(Object l, Object r);
abstract Object prod(Object l, Object r);
@Override
public Object forPlus(Expr l, Expr r) {
return plus(l.accept(this), r.accept(this));
}
@Override
public Object forDiff(Expr l, Expr r) {
return diff(l.accept(this), r.accept(this));
}
@Override
public Object forProd(Expr l, Expr r) {
return prod(l.accept(this), r.accept(this));
}
@Override
public Object forConst(Object c) {
return c;
}
}Eval is still an abstract class. This is because how to evaluate numeric expressions is different from set expressions. In particular, as the code says, the differences are how to actually do + - and x.
Let’s first define the IntEval for evaluating numeric expressions.
class IntEval extends Eval {
@Override
Object plus(Object l, Object r) {
return (Integer) l + (Integer) r;
}
@Override
Object diff(Object l, Object r) {
return (Integer) l - (Integer) r;
}
@Override
Object prod(Object l, Object r) {
return (Integer) l * (Integer) r;
}
}This is easy. The code says we can just use plain numeric operations.
By now, we are able to evaluate the numeric expressions.
(Integer) new Plus(new Const(1), new Const(2)).accept(new IntEval());Now let’s implement the same for set expressions.
First, let’s define the classes for representing set:
abstract class Set {
Set add(Integer i) {
if (mem(i)) {
return this;
} else {
return new Add(i, this);
}
}
abstract boolean mem(Integer i);
abstract Set plus(Set s);
abstract Set diff(Set s);
abstract Set prod(Set s);
}
class Empty extends Set {
@Override
boolean mem(Integer i) {
return false;
}
@Override
Set plus(Set s) {
return s;
}
@Override
Set diff(Set s) {
return new Empty();
}
@Override
Set prod(Set s) {
return new Empty();
}
}
class Add extends Set {
private Integer i;
private Set s;
Add(Integer i, Set s) {
this.i = i;
this.s = s;
}
@Override
boolean mem(Integer i) {
if (i.equals(this.i)) {
return true;
} else {
return s.mem(i);
}
}
@Override
Set plus(Set s) {
return this.s.plus(s.add(i));
}
@Override
Set diff(Set s) {
if (s.mem(i)) {
return this.s.diff(s);
} else {
return this.s.diff(s).add(i);
}
}
@Override
Set prod(Set s) {
if (s.mem(i)) {
return this.s.prod(s).add(i);
} else {
return this.s.prod(s);
}
}
}The interesting part here is probably Add. Let’s see how a set is constructed:
First we start with an empty set:
{}
Let’s add 1 to it:
(1 {})
Let’s add 2 to it:
(2 (1 {}))
So on and so forth.
So you can see this is not the most correct way of implementing a set, but it only serves the purpose of teaching.
Then, the SetEval becomes a no brainer.
class SetEval extends Eval {
@Override
Object plus(Object l, Object r) {
return ((Set)l).plus((Set)r);
}
@Override
Object diff(Object l, Object r) {
return ((Set)l).diff((Set)r);
}
@Override
Object prod(Object l, Object r) {
return ((Set)l).prod((Set)r);
}
}Now we can try to evaluate a set expression:
(Set) new Prod(new Const(new Empty().add(7)), new Const(new Empty().add(3))).accept(new SetEval());Edit: I just finished reading this book the second time, and converted most of the code to Kotlin.
import java.util.*
import kotlin.math.sqrt
abstract class Point(val x: Int, val y: Int) {
abstract fun distanceToO(): Double
fun closerToO(p: Point) = distanceToO() < p.distanceToO()
fun minus(p: Point) = CartesianPt(x - p.x, y - p.y)
}
open class CartesianPt(x: Int, y: Int) : Point(x, y) {
override fun distanceToO() = sqrt((x * x + y * y).toDouble())
}
open class ManhattanPt(x: Int, y: Int) : Point(x, y) {
override fun distanceToO() = (x + y).toDouble()
}
class ShadowedManhattanPt(x: Int, y: Int, private val dx: Int, private val dy: Int) : ManhattanPt(x, y) {
override fun distanceToO() = (super.distanceToO() + dx + dy)
}
class ShadowedCartesianPt(x: Int, y: Int, private val dx: Int, private val dy: Int) : CartesianPt(x, y) {
override fun distanceToO() = CartesianPt(x + dx, y + dy).distanceToO()
}
abstract class Layer
class Base(val o: Any) : Layer()
class Slice(val l: Layer) : Layer()
abstract class Shish {
val ooFn = OnlyOnionsVisitor()
val ivFn = IsVegetarianVisitor()
abstract fun onlyOnions(): Boolean
abstract fun isVegetarian(): Boolean
}
class Skewer : Shish() {
override fun onlyOnions() = ooFn.forSkewer()
override fun isVegetarian() = ivFn.forSkewer()
}
class Onion(val s: Shish) : Shish() {
override fun onlyOnions() = ooFn.forOnion(s)
override fun isVegetarian() = ivFn.forOnion(s)
}
class Lamb(val s: Shish) : Shish() {
override fun onlyOnions() = ooFn.forLamb(s)
override fun isVegetarian() = ivFn.forLamb(s)
}
class Tomato(val s: Shish) : Shish() {
override fun onlyOnions() = ooFn.forTomato(s)
override fun isVegetarian() = ivFn.forTomato(s)
}
class OnlyOnionsVisitor {
fun forSkewer() = true
fun forOnion(s: Shish) = s.onlyOnions()
fun forLamb(s: Shish) = false
fun forTomato(s: Shish) = false
}
class IsVegetarianVisitor {
fun forSkewer() = true
fun forOnion(s: Shish) = s.isVegetarian()
fun forLamb(s: Shish) = false
fun forTomato(s: Shish) = s.isVegetarian()
}
abstract class Kebab {
abstract fun isVeggie(): Boolean
abstract fun whatHolder(): Any
}
class Holder(private val o: Any) : Kebab() {
override fun isVeggie() = true
override fun whatHolder() = o
}
class Shallot(private val k: Kebab) : Kebab() {
override fun isVeggie() = k.isVeggie()
override fun whatHolder() = k.whatHolder()
}
class Shrimp(private val k: Kebab) : Kebab() {
override fun isVeggie() = false
override fun whatHolder() = k.whatHolder()
}
class Radish(private val k: Kebab) : Kebab() {
override fun isVeggie() = k.isVeggie()
override fun whatHolder() = k.whatHolder()
}
class Pepper(private val k: Kebab) : Kebab() {
override fun isVeggie() = k.isVeggie()
override fun whatHolder() = k.whatHolder()
}
abstract class Rod
class Dagger : Rod()
class Sabre : Rod()
class Sword : Rod()
abstract class Plate
class Gold : Plate()
class Silver : Plate()
class Brass : Plate()
class Copper : Plate()
class Wood : Plate()
abstract class Pizza {
val remFn = RemoveAnchovyVisitor()
val topFn = TopAnchovyWithCheeseVisitor()
val subFn = SubstituteAnchovyByCheeseVisitor()
abstract fun removeAnchovy(): Pizza
abstract fun topAnchovyWithCheese(): Pizza
abstract fun substituteAnchovyByCheese(): Pizza
}
class SubstituteAnchovyByCheeseVisitor {
fun forCrust() = Crust()
fun forCheese(p: Pizza) = Cheese(p.substituteAnchovyByCheese())
fun forOlive(p: Pizza) = Olive(p.substituteAnchovyByCheese())
fun forAnchovy(p: Pizza) = Cheese(p.substituteAnchovyByCheese())
fun forSausage(p: Pizza) = Sausage(p.substituteAnchovyByCheese())
fun forSpinach(p: Pizza) = Spinach(p.substituteAnchovyByCheese())
}
class TopAnchovyWithCheeseVisitor {
fun forCrust() = Crust()
fun forCheese(p: Pizza) = Cheese(p.topAnchovyWithCheese())
fun forOlive(p: Pizza) = Olive(p.topAnchovyWithCheese())
fun forAnchovy(p: Pizza) = Cheese(Anchovy(p.topAnchovyWithCheese()))
fun forSausage(p: Pizza) = Sausage(p.topAnchovyWithCheese())
fun forSpinach(p: Pizza) = Spinach(p.topAnchovyWithCheese())
}
class RemoveAnchovyVisitor {
fun forCrust() = Crust()
fun forCheese(p: Pizza) = Cheese(p.removeAnchovy())
fun forOlive(p: Pizza) = Olive(p.removeAnchovy())
fun forAnchovy(p: Pizza) = p.removeAnchovy()
fun forSausage(p: Pizza) = Sausage(p.removeAnchovy())
fun forSpinach(p: Pizza) = Spinach(p.removeAnchovy())
}
class Crust : Pizza() {
override fun removeAnchovy() = remFn.forCrust()
override fun topAnchovyWithCheese() = topFn.forCrust()
override fun substituteAnchovyByCheese() = subFn.forCrust()
}
class Cheese(val p: Pizza) : Pizza() {
override fun removeAnchovy() = remFn.forCheese(p)
override fun topAnchovyWithCheese() = topFn.forCheese(p)
override fun substituteAnchovyByCheese() = subFn.forCheese(p)
}
class Olive(val p: Pizza) : Pizza() {
override fun removeAnchovy() = remFn.forOlive(p)
override fun topAnchovyWithCheese() = topFn.forOlive(p)
override fun substituteAnchovyByCheese() = subFn.forOlive(p)
}
class Anchovy(val p: Pizza) : Pizza() {
override fun removeAnchovy() = remFn.forAnchovy(p)
override fun topAnchovyWithCheese() = topFn.forAnchovy(p)
override fun substituteAnchovyByCheese() = subFn.forAnchovy(p)
}
class Sausage(val p: Pizza) : Pizza() {
override fun removeAnchovy() = remFn.forSausage(p)
override fun topAnchovyWithCheese() = topFn.forSausage(p)
override fun substituteAnchovyByCheese() = subFn.forSausage(p)
}
class Spinach(val p: Pizza) : Pizza() {
override fun removeAnchovy(): Pizza = remFn.forSpinach(p)
override fun topAnchovyWithCheese() = topFn.forSpinach(p)
override fun substituteAnchovyByCheese() = subFn.forSpinach(p)
}
abstract class Pie {
abstract fun accept(ask: PieVisitor): Pie
}
interface PieVisitor {
fun forBot(): Pie
fun forTop(t: Any, r: Pie): Pie
}
class RemV(private val o: Any) : PieVisitor {
override fun forBot() = Bot()
override fun forTop(t: Any, r: Pie) =
if (o == t)
r.accept(this)
else Top(t, r.accept(this))
}
open class SubstV(private val n: Any, private val o: Any): PieVisitor {
override fun forBot() = Bot()
override fun forTop(t: Any, r: Pie) =
if (o == t)
Top(n, r.accept(this))
else Top(t, r.accept(this))
}
class LtdSubstV(private val c: Int, private val n: Any, private val o: Any) : SubstV(n, o) {
override fun forTop(t: Any, r: Pie) =
if (c == 0) {
Top(t, r)
} else if (o == t) {
Top(n, r.accept(LtdSubstV(c - 1, n, o)))
} else {
Top(t, r.accept(this))
}
}
class Bot : Pie() {
override fun accept(ask: PieVisitor) = ask.forBot()
override fun toString(): String {
return "Bottom |"
}
}
class Top(private val t: Any, private val r: Pie) : Pie() {
override fun accept(ask: PieVisitor) = ask.forTop(t, r)
override fun toString(): String {
return "$t <<< $r"
}
}
abstract class Fish
class Anchovy2 : Fish() {
override fun equals(other: Any?): Boolean {
if (this === other) return true
if (javaClass != other?.javaClass) return false
return true
}
override fun hashCode(): Int {
return javaClass.hashCode()
}
}
class Salmon : Fish() {
override fun equals(other: Any?): Boolean {
if (this === other) return true
if (javaClass != other?.javaClass) return false
return true
}
override fun hashCode(): Int {
return javaClass.hashCode()
}
}
class Tuna : Fish() {
override fun equals(other: Any?): Boolean {
if (this === other) return true
if (javaClass != other?.javaClass) return false
return true
}
override fun hashCode(): Int {
return javaClass.hashCode()
}
}
abstract class Fruit
class Peach : Fruit() {
override fun equals(other: Any?): Boolean {
return other is Peach
}
}
class Apple : Fruit() {
override fun equals(other: Any?): Boolean {
return other is Apple
}
}
class Pear : Fruit() {
override fun equals(other: Any?): Boolean {
return other is Pear
}
}
class Lemon : Fruit() {
override fun equals(other: Any?): Boolean {
return other is Lemon
}
}
class Fig : Fruit() {
override fun equals(other: Any?): Boolean {
return other is Fig
}
}
abstract class Tree {
abstract fun accept(ask: TreeVisitor): Any
}
class Bud : Tree() {
override fun accept(ask: TreeVisitor) = ask.forBud()
}
class Flat(private val f: Fruit, private val t: Tree) : Tree() {
override fun accept(ask: TreeVisitor) = ask.forFlat(f, t)
}
class Split(private val l: Tree, private val r: Tree) : Tree() {
override fun accept(ask: TreeVisitor) = ask.forSplit(l, r)
}
interface TreeVisitor {
fun forBud(): Any
fun forFlat(f: Fruit, t: Tree): Any
fun forSplit(l: Tree, r: Tree): Any
}
class IsFlat : TreeVisitor {
override fun forBud() = true
override fun forFlat(f: Fruit, t: Tree) = t.accept(this)
override fun forSplit(l: Tree, r: Tree) = false
}
class IsSplit : TreeVisitor {
override fun forBud() = true
override fun forFlat(f: Fruit, t: Tree) = false
override fun forSplit(l: Tree, r: Tree) = (l.accept(this) as Boolean) && (r.accept(this) as Boolean)
}
class Occurs(private val a: Fruit) : TreeVisitor {
override fun forBud() = 0
override fun forFlat(f: Fruit, t: Tree) =
if (a == f) {
(t.accept(this) as Int) + 1
} else {
t.accept(this)
}
override fun forSplit(l: Tree, r: Tree) = (l.accept(this) as Int) + (r.accept(this) as Int)
}
abstract class Expr {
abstract fun accept(ask: ExprVisitor): Any
}
class Plus(private val l: Expr, private val r: Expr) : Expr() {
override fun accept(ask: ExprVisitor) = ask.forPlus(l, r)
}
class Diff(private val l: Expr, private val r: Expr) : Expr() {
override fun accept(ask: ExprVisitor) = ask.forDiff(l, r)
}
class Prod(private val l: Expr, private val r: Expr) : Expr() {
override fun accept(ask: ExprVisitor) = ask.forProd(l, r)
}
class Const(private val c: Any) : Expr() {
override fun accept(ask: ExprVisitor) = ask.forConst(c)
}
interface ExprVisitor {
fun forPlus(l: Expr, r: Expr): Any
fun forDiff(l: Expr, r: Expr): Any
fun forProd(l: Expr, r: Expr): Any
fun forConst(c: Any): Any
}
abstract class Eval : ExprVisitor {
override fun forPlus(l: Expr, r: Expr) = plus(l.accept(this), r.accept(this))
override fun forDiff(l: Expr, r: Expr) = diff(l.accept(this), r.accept(this))
override fun forProd(l: Expr, r: Expr) = prod(l.accept(this), r.accept(this))
override fun forConst(c: Any) = c
abstract fun plus(l: Any, r: Any): Any
abstract fun diff(l: Any, r: Any): Any
abstract fun prod(l: Any, r: Any): Any
}
class IntEval : Eval() {
override fun plus(l: Any, r: Any) = l as Int + r as Int
override fun diff(l: Any, r: Any) = l as Int - r as Int
override fun prod(l: Any, r: Any) = l as Int * r as Int
}
abstract class Set {
fun add(i: Int) = if (mem(i)) this else Add(i, this)
abstract fun mem(n: Int): Boolean
abstract fun plus(t: Set): Set
abstract fun diff(t: Set): Set
abstract fun prod(t: Set): Set
}
class Empty : Set() {
override fun mem(n: Int) = false
override fun plus(t: Set) = t
override fun diff(t: Set) = Empty()
override fun prod(t: Set) = Empty()
override fun toString() = "."
}
class Add(private val i: Int, private val s: Set) : Set() {
override fun mem(n: Int) = if (i == n) true else s.mem(n)
override fun plus(t: Set) = s.plus(t.add(i))
override fun diff(t: Set) = if (t.mem(i)) s.diff(t) else s.diff(t).add(i)
override fun prod(t: Set) = if (t.mem(i)) s.prod(t).add(i) else s.prod(t)
override fun toString() = "$i $s"
}
class SetEval : Eval() {
override fun plus(l: Any, r: Any) = (l as Set).plus(r as Set)
override fun diff(l: Any, r: Any) = (l as Set).diff(r as Set)
override fun prod(l: Any, r: Any) = (l as Set).prod(r as Set)
}
abstract class Shape {
abstract fun accept(ask: ShapeVisitor): Boolean
}
class Circle(private val r: Int) : Shape() {
override fun accept(ask: ShapeVisitor) = ask.forCircle(r)
}
class Square(private val s: Int) : Shape() {
override fun accept(ask: ShapeVisitor) = ask.forSquare(s)
}
class Trans(private val q: Point, private val s: Shape) : Shape() {
override fun accept(ask: ShapeVisitor) = ask.forTrans(q, s)
}
class Union(private val s: Shape, private val t: Shape) : Shape() {
override fun accept(ask: ShapeVisitor) = (ask as UnionVisitor).forUnion(s, t)
}
interface ShapeVisitor {
fun forCircle(r: Int): Boolean
fun forSquare(s: Int): Boolean
fun forTrans(q: Point, s: Shape): Boolean
}
interface UnionVisitor : ShapeVisitor {
fun forUnion(s: Shape, t: Shape): Boolean
}
open class HasPt(private val p: Point) : ShapeVisitor {
override fun forCircle(r: Int) = p.distanceToO() <= r
override fun forSquare(s: Int) = p.x <= s && p.y <= s
open fun newHasPt(p: Point) = HasPt(p)
override fun forTrans(q: Point, s: Shape) = s.accept(newHasPt(p.minus(q)))
}
class UnionHasPt(p: Point) : HasPt(p), UnionVisitor {
override fun newHasPt(p: Point) = UnionHasPt(p)
override fun forUnion(s: Shape, t: Shape) = s.accept(this) || t.accept(this)
}
abstract class PieD {
abstract fun accept(ask: PieVisitorI): Any
}
class Bot2 : PieD() {
override fun accept(ask: PieVisitorI) = ask.forBot()
}
class Top2(private val t: Any, private val r: PieD) : PieD() {
override fun accept(ask: PieVisitorI) = ask.forTop(t, r)
}
interface PieVisitorI {
fun forBot(): Any
fun forTop(t: Any, r: PieD): Any
}
class OccursV(private val a: Any) : PieVisitorI {
override fun forBot() = 0
override fun forTop(t: Any, r: PieD) =
if (t == a) {
r.accept(this) as Int + 1
} else {
r.accept(this)
}
}
class SubstV2(private val n: Any, private val o: Any) : PieVisitorI {
override fun forBot() = Bot()
override fun forTop(t: Any, r: PieD) =
if (o == t)
Top2(n, r.accept(this) as PieD)
else
Top2(t, r.accept(this) as PieD)
}
class RemV2(private val o: Any) : PieVisitorI {
override fun forBot() = Bot()
override fun forTop(t: Any, r: PieD) =
if (t == o)
r.accept(this)
else
Top2(t, r.accept(this) as PieD)
}
interface PiemanI {
fun addTop(t: Any): Int
fun remTop(t: Any): Int
fun substTop(n: Any, o: Any): Int
fun occTop(o: Any): Int
}
class PiemanM : PiemanI {
private var p: PieD = Bot2()
override fun addTop(t: Any): Int {
p = Top2(t, p)
return occTop(t)
}
override fun remTop(t: Any): Int {
p = p.accept(RemV2(t)) as PieD
return occTop(t)
}
override fun substTop(n: Any, o: Any): Int {
p = p.accept(SubstV2(n, o)) as PieD
return occTop(n)
}
override fun occTop(o: Any) = p.accept(OccursV(o)) as Int
}
fun main(args: Array<String>) {
// println(ManhattanPt(3, 4).distanceToO())
// println(CartesianPt(3, 4).distanceToO())
// println(Top(Anchovy2(), Top(Salmon(), Top(Anchovy2(), Top(Tuna(), Bot())))).accept(RemoveVisitor(Anchovy2())))
// println(Top(Anchovy2(), Top(Salmon(), Top(Anchovy2(), Top(Tuna(), Bot())))).accept(SubstituteVisitor(Anchovy2(), Salmon())))
// println(Top(Anchovy2(), Top(Anchovy2(), Top(Anchovy2(), Top(Tuna(), Bot())))).accept(LtdSubstituteVisitor(2, Salmon(), Anchovy2())))
// println(Plus(Prod(Const(1), Const(2)), Const(3)).accept(IntEval()))
// println(Plus(Prod(Const(Empty().add(1).add(2)), Const(Empty().add(2).add(3))), Const(Empty().add(3))).accept(SetEval()))
Trans(
CartesianPt(3, 7),
Union(
Square(10),
Circle(10)
)
).accept(UnionHasPt(CartesianPt(13, 17)))
}
Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Email